Introduction: Unlock the Power of Calculus on Your Graphing Calculator
The TI-84 graphing calculator is an indispensable tool for students and professionals in the field of calculus. Its ability to perform complex calculations, including integrals, makes it an invaluable companion for solving problems and exploring mathematical concepts. This comprehensive guide will provide a step-by-step walkthrough of how to use the TI-84’s integral feature, empowering you to harness the full potential of this powerful tool.

Understanding the Concept of Integrals
Integrals are a fundamental concept in calculus that represent the area under a curve or the accumulation of a function over a given interval. They are widely used in various scientific and engineering disciplines, from calculating volumes to finding work done by a force.
Using the TI-84 to Calculate Integrals
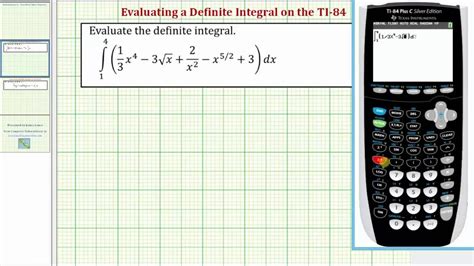
Step 1: Entering the Function
- Press the “Y=” button to access the function editor.
- Enter the expression for the function you want to integrate.
Step 2: Setting the Integration Bounds
- Press the “Window” button to adjust the graphing window settings.
- Set the “xmin” and “xmax” values to define the lower and upper bounds of integration.
Step 3: Using the Integral Command
- Press the “Math” button and select the “Calculus” submenu.
- Choose “fnInt” (for definite integrals) or “∫” (for indefinite integrals).
- Enter the function and specify the integration bounds.
- Press “Enter” to obtain the result.
Advanced Integral Features
Definite Integrals:
- Calculate the area under a curve using “fnInt” (definite integral).
- Specify lower and upper bounds to calculate the exact area.
Indefinite Integrals:
- Find antiderivatives using “∫” (indefinite integral).
- Leave the integration bounds blank to obtain a general expression.
Numerical Integration:
- Estimate the value of an integral without a closed-form solution using “fMin” or “fMax” (numerical integration).
- Set the “step” value to control the accuracy of the estimation.
Applications of Integrals in Real-World Scenarios
Integrals find countless applications in the sciences and engineering, including:
- Volumes of Solids of Revolution: Determine the volume of a solid generated by rotating a curve around an axis.
- Work Done by a Force: Calculate the work done by a constant or variable force over a given distance.
- Net Change: Find the net change in a quantity over a time interval, such as population growth or speed accumulation.
- Fluid Flow: Determine the rate of fluid flow or the volume of fluid passing through a pipe.
Overcoming Challenges: Pain Points and Motivations
Pain Points:
- Complex Integrals: Some integrals may not have closed-form solutions and require numerical integration or approximation.
- Integration by Parts: Manually performing integration by parts can be tedious and error-prone.
- Trigonometric and Logarithmic Integrals: Dealing with trigonometric or logarithmic functions in integrals can add complexity.
Motivations:
- Academic Success: Calculus students rely on integrals for solving complex problems and understanding mathematical concepts.
- Professional Applications: Engineers, scientists, and researchers use integrals to solve real-world problems.
- Curiosity and Exploration: Integrals open up a world of mathematical exploration and discovery.
Tips and Tricks: Enhancing Your Integral Prowess
- Approximating Integrals: Use numerical integration for integrals without exact solutions.
- Using the Derivative: Check your indefinite integrals by differentiating the result.
- Integration by Substitution: Break down complex integrals by substituting variables.
- Trigonometric Identities: Leverage trigonometric identities to simplify integrals involving trigonometric functions.
- Get Help: Refer to online resources, textbooks, or your instructor for additional assistance.
Common Mistakes to Avoid: Pitfalls to Watch Out for
- Incorrect Integration Bounds: Double-check the lower and upper bounds of integration.
- Forgetting the Constant of Integration: When finding indefinite integrals, always add the constant of integration “+C”.
- Neglecting the Absolute Value: If the integrand involves absolute values, ensure you include them in the integral.
- Improper Substitutions: Verify that your substitutions are valid and lead to a correct solution.
- Division by Zero: Avoid integrating functions that result in division by zero.
Conclusion: Unleashing the Power of Integrals
Mastering the integral feature on the TI-84 calculator is a game-changer for calculus students and professionals. By understanding the concept of integrals, utilizing the TI-84’s advanced features, overcoming challenges, and leveraging helpful tips and tricks, you can harness the power of this tool to solve complex problems, explore mathematical concepts, and make valuable contributions in your field.