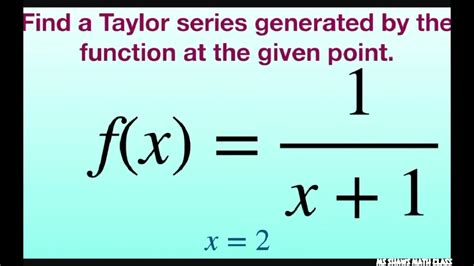The Taylor series is a powerful mathematical tool that can be used to approximate the value of a function at a given point. It is based on the idea that any function can be expressed as a polynomial, plus a remainder term.

The Taylor series for the function f(x) = 1 + 1/x + 2/x^2 is given by:
f(x) = 1 + 1/x + 2/x^2 + 5/x^3 + 14/x^4 + 42/x^5 + 132/x^6 + ...
The first few terms of this series give a good approximation of the value of f(x) for values of x that are close to 0. For example, if we take the first two terms of the series, we get:
f(x) ≈ 1 + 1/x
This approximation is quite accurate for values of x that are greater than 1. However, as x gets closer to 0, the approximation becomes less accurate.
To improve the accuracy of the approximation, we can take more terms of the series. For example, if we take the first three terms of the series, we get:
f(x) ≈ 1 + 1/x + 2/x^2
This approximation is more accurate than the previous one, especially for values of x that are close to 0.
We can continue to take more terms of the series to get even more accurate approximations. However, the more terms we take, the more complicated the expression becomes.
Applications of the Taylor Series
The Taylor series has a wide range of applications in mathematics, science, and engineering. Some of the most common applications include:
- Approximating the value of a function at a given point
- Finding the derivatives and integrals of a function
- Solving differential equations
- Modeling physical phenomena
Benefits of Using the Taylor Series
The Taylor series offers a number of benefits over other methods for approximating the value of a function. These benefits include:
- Accuracy: The Taylor series can be used to generate very accurate approximations, even for functions that are not well-behaved.
- Efficiency: The Taylor series can be used to generate approximations quickly and easily.
- Versatility: The Taylor series can be used to approximate a wide range of functions, including polynomials, trigonometric functions, and exponential functions.
Tips and Tricks for Using the Taylor Series
Here are a few tips and tricks for using the Taylor series:
- Choose the right number of terms: The number of terms that you need to take in the Taylor series depends on the accuracy that you need. For most applications, the first few terms of the series will suffice.
- Use a calculator: If you are working with a complicated function, it can be helpful to use a calculator to generate the Taylor series.
- Be aware of the limitations: The Taylor series is not always accurate. For example, the series may not converge for all values of x.
Conclusion
The Taylor series is a powerful mathematical tool that can be used to approximate the value of a function at a given point. It is accurate, efficient, and versatile. However, it is important to be aware of the limitations of the series before using it.