Finding Slope from a Graph Worksheet

Introduction

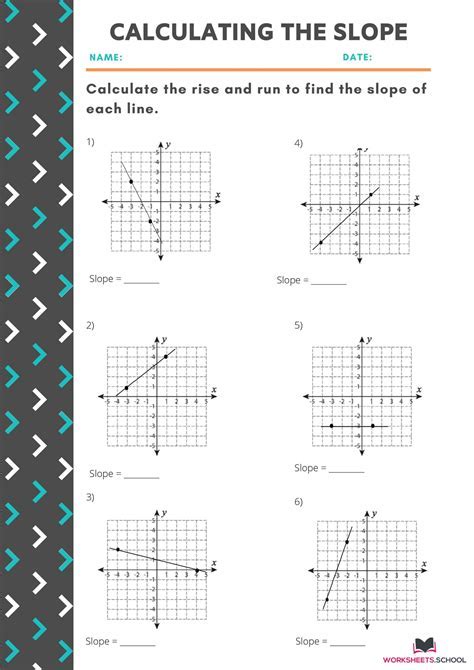
Slope is a measure of how steep a line is. It is calculated by dividing the change in y by the change in x. In other words, it is the ratio of the vertical change to the horizontal change. Slope can be positive, negative, or zero.

Slope is an important concept in mathematics. It is used to describe the rate of change of a function, the steepness of a line, and the direction of a vector. Slope is also used in a variety of applications, such as engineering, physics, and economics.

How to Find Slope from a Graph

There are two common methods for finding the slope of a line from a graph:

The rise-over-run method
The two-point method

The Rise-over-Run Method

The rise-over-run method is the most straightforward way to find the slope of a line. To use this method, simply count the number of units the line rises (the vertical change) and the number of units the line runs (the horizontal change). Then, divide the rise by the run.

For example, consider the following line:

[Image of a line with a positive slope]

To find the slope of this line using the rise-over-run method, we would count the number of units the line rises (4) and the number of units the line runs (3). Then, we would divide the rise by the run to get the slope:

slope = rise / run
slope = 4 / 3
slope = 1.33

The Two-Point Method

The two-point method is another common way to find the slope of a line. To use this method, simply choose two points on the line and calculate the slope using the following formula:

slope = (y2 - y1) / (x2 - x1)

where:

(x1, y1) is the first point
(x2, y2) is the second point

For example, consider the following line:

[Image of a line with a negative slope]

To find the slope of this line using the two-point method, we could choose the points (1, 2) and (3, 0). Then, we would calculate the slope using the formula above:

slope = (y2 - y1) / (x2 - x1)
slope = (0 - 2) / (3 - 1)
slope = -1

Applications of Slope

Slope is a versatile concept with a wide range of applications in various fields. Here are a few examples:

Engineering: Slope is used to calculate the steepness of ramps, bridges, and other structures.
Physics: Slope is used to describe the velocity of objects in motion.
Economics: Slope is used to measure the rate of change of economic variables, such as inflation and unemployment.

Conclusion

Slope is a fundamental concept in mathematics with a variety of applications in different fields. By understanding how to find the slope of a line from a graph, you can gain a deeper understanding of the world around you.

Worksheet

To practice finding slope from a graph, try completing the following worksheet:

Find the slope of the line that passes through the points (1, 2) and (3, 6).
Find the slope of the line that has the equation y = 2x + 1.
Find the slope of the line that is perpendicular to the line that passes through the points (1, 2) and (3, 6).